| |
| | |  | blättern ( 8 / 21 ) |  |
| |
A - Schlüsselbegriffe und Grundannahmen der realen Nachfragentheorie |
| |
Die distributiven Koeffizienten als Grundlage des Kreislaufmodells 3.0 |
| |
|
|
|
| |
|
Das Modell ist häufig „schlauer“ als sein Anwender. Damit meine ich Folgendes: Sobald man gezwungen ist, seine Gedanken zu ordnen und in den systematischen Rahmen eines kohärenten (d. h. widerspruchsfreien) Modells zu stellen, wird man nolens volens zu Schlussfolgerungen gedrängt, die man eigentlich nie im Sinn hatte, oder man wird sogar gezwungen, liebgewordene Überzeugungen aufzugeben. Deshalb ist jemand, der ein noch so einfaches und trivial klingendes ökonomisches Modell begriffen hat, häufig auf eine bestimmte Art weitaus klüger als jemand, der tausend Fakten parat hat, viele schöne Anekdoten zu erzählen vermag und mit großen Worten um sich zu werfen versteht, jedoch über keinen kohärenten, die Gedanken ordnenden, disziplinierenden Rahmen verfügt. |
|
| |
|
Paul Krugman, bekannter amerikanischer Ökonom (Nobelpreisträger 2008) |
|
|
|
|
|
Heben wir noch einmal hervor, dass das erste Modell des allgemeinen Gleichgewichts (v 1.0), also das Kreislaufmodell von Quesnay, ein authentisches Modell der Wirtschaftswissenschaft war. Es wurde nicht von irgendwo abgekupfert - wie etwas das Modell von Walras und Pareto und manche andere späteren neoliberalen Ansätze -, sondern es war wirklich eine selbstständige Schöpfung der Wirtschaftswissenschaft. Das erste Kreislaufmodell (v 1.0) hatte eine tabellarische Struktur, die sich eigentlich leicht - heute scheint uns dies zumindest so - in mathematische Gleichungen umschreiben lässt. Trotzdem dauerte es fast zwei Jahrhunderte, bis dies getan wurde. Offensichtlich brauchte man eine Idee, wie man den Kreislauf mathematisieren kann. Ich bezeichne diese weitere analytische Stufe der ökonomischen Kreislauftheorie als die Version 2.x.
Die ideelle Grundlage der ersten mathematischen Konzeption des Kreislaufsmodells, die aus den Arbeiten des Neoricardianers Piero Sraffa (Production of Commodities by Means of Commodities, 1960) hervorgegangen ist, waren die technischen Koeffizienten. Durch sie wurde das Kreislaufmodell mikroökonomisch fundiert, und zwar im Bereich der Produktion. Schon daran unterscheidet sich dieses Modell völlig vom neoliberalen partikel-mechanischen. Zugleich bedeutete es eine völlig andere Wahrnehmung bzw. Auffassung dessen, wie die Produktion zustande kommt und was sie bedeutet. In dem neoliberalen partikel-mechanischen Modell wählt der produzierende Unternehmer zwischen einzelnen Produktionsfaktoren. Er entscheidet sich für diejenigen einzelnen Faktoren, die „am produktivsten“ sind. Die sogenannte „Produktivität“ eines einzelnen Produktionsfaktors ist ein metaphysischer Unsinn aus dem 19. bzw. 18. Jahrhundert, wie wir schon festgestellt haben, aber wir werden dazu noch mehr sagen. Jetzt geht es nur darum, hervorzuheben, dass in dem Kreislaufmodell der Unternehmer nicht zwischen verschiedenen (einzelnen) Produktionsfaktoren wählt, sondern zwischen verschiedenen technischen Kombinationen, die durch technische Koeffizienten quantitativ genau spezifiziert werden. Man kann den prinzipiellen Unterschied zwischen diesen zwei Auffassungen pointiert auch so ausdrücken: Nach dem neoliberalen Modell entscheiden Unternehmer alleine mit ihrem Buchhalter, nach dem Kreislaufmodell benötigen sie auch noch ihren Technologen.
Die technischen Kombinationen informieren darüber, welche Güter in welchen Mengen benötigt werden, um ein bestimmtes Gut herzustellen. Man kann sie sich als Kochrezepte vorstellen. Wenn der Unternehmer mehrere „Kochrezepte“ bzw. Koeffizientensätze hat, nach denen er ein bestimmtes Produkt herstellen kann, dann lässt er sie nach den gültigen Preisen ausrechen, um die billigste Alternative herauszufinden. Als alle Unternehmer auf diese Weise ihre Entscheidungen treffen, nachdem die billigste Kombination jedes Unternehmen bekannt ist, lässt sich - mit den technischen Koeffizienten als Konstanten - ein System von Gleichungen schreiben, die dann die Wirtschaft als ein Ganzes erfassen. Wenn man ein solches Gleichungssystem hat, kann man die Mathematik weiter anwenden und zu verschiedenen Schlussfolgerungen über die Gesetzmäßigkeiten in der Wirtschaft kommen. Diese Schlussfolgerungen sind dann völlig andere, als die des neoliberalen Modells, wo nicht die Kombinationen, sondern die Produktionsgüter einzeln die elementaren Bestandteile der Entscheidungen sind.
Wir haben bei der Untersuchung des Marxschen Transformationsproblems aber nicht die technischen, sondern die distributiven Koeffizienten benutzt. Die distributiven Koeffizienten spezifizieren, wie ein Sektor seine Produktion verteilt. Es sind Zahlen, die uns wissen lassen, welchen relativen Anteil der ganzen Produktion ein Sektor an einen anderen liefert. Die technischen Koeffizienten bestimmen also die Inputseite, die distributiven Koeffizienten die Outputseite der Sektoren. Manchmal ist es möglich, aus den technischen Koeffizienten distributive direkt auszurechnen und umgekehrt, aber nicht immer. Einer dieser (mathematisch) einfachen Fälle ist der stationäre Zustand, den wir auch bei der Untersuchung des Transformationsproblems angenommen hatten. Wir konnten uns dort frei entscheiden, mit welchen Koeffizienten wir arbeiten wollten. Manchmal ist man aber gezwungen, nur die einen, oder die anderen, oder sogar beide Koeffizientenarten zu benutzen, um zu einem Ergebnis zu kommen.
Die Kreislaufmodelle und die Mathematik
Wenn wir schon von der historischen Entwicklung der kreislauftheoretischen Analyse sprechen, ist es angebracht der Frage nachzugehen, warum es so lange gedauert hat, bis man darauf gekommen ist, wie man das Kreislaufmodell mathematisch formulieren kann. Hier lässt sich zwischen allgemeinen und besonderen Gründen unterscheiden.
Den allgemeinen Grund haben wir bereits angedeutet: Wenn man einen Prozess mathematisch erfassen will, reicht es nicht aus, dass man sich mit der Mathematik gut auskennt. Man muss eine problematikbezogene Idee haben, auf die man dann die Mathematik anwendet. Das wissen wir allzu gut aus den Naturwissenschaften und vor allem aus den technischen Wissenschaften, für die die mathematische Sprache bei Weitem die wichtigste ist. Marx fehlte eine solche Idee, so dass ihm seine mathematischen Kenntnisse, die eigentlich solide waren, nichts nutzten. Anstatt diese zu suchen, hat er sich für seine Reproduktionsschemata immer neue numerische Beispiele ausgedacht, so dass er nichts als nur einen Zahlensalat hinterlassen hat, an dem sich dann auch Generationen abgearbeitet haben.
Woher eine neue Idee kommt, ist eine bis heute nicht zufrieden stellend beantwortete Frage der Erkenntnistheorie. Wir wissen immer noch nicht, warum uns manchmal etwas Originelles einfällt und dann eine lange Zeit nichts mehr. Die Erklärung, die originellen Einfälle wären das Ergebnis von Zufall und Glück, stimmt irgendwie immer, aber ob damit wirklich etwas erklärt wird, daran lässt sich sehr zweifeln.
Eine originelle Idee hat bestimmt auch etwas mit der Ausbildung zu tun, aber nicht viel. Die Ausbildung ist nur eine Voraussetzung für den wissenschaftlichen Fortschritt, seine treibende Kraft und seine Ursache ist sie bestimmt nicht. Marx ist das beste Beispiel dafür, dass die Ausbildung und die Intelligenz nicht automatisch auch Kreativität bedeuten. Eigentlich ist die ganze Wirtschaftswissenschaft ein exzellentes Beispiel einer Wissenschaft, der seit zwei Jahrhunderten vielleicht einige wenige kleine, aber keine revolutionäre Ideen eingefallen sind. Dies mag der wichtigste Grund dafür zu sein, warum sie alle Ideen und alle Ansätze, die zuerst in den Naturwissenschaften formuliert worden sind, eifrig nachäfft.
Zu den besonderen und konkreten Gründen, warum das Kreislaufmodell zwei Jahrhunderte nach Quesnay keine analytische bzw. mathematische Weiterentwicklung erfahren hat, lassen sich mehrere anführen. Es kann auch damit zu tun haben, dass die Kreislauftheorie von Marx theoretisch „besetzt“ worden ist, so dass die Reichen und Herrschenden im Kapitalismus andere Modelle ideologisch gefordert und finanziell unterstützt haben. Eine noch schwierigere Position hatten die marxistischen Ökonomen in den ehemaligen kommunistischen Ländern. Dort haben die Machthaber den Marxismus zum Dogma erklärt und nie etwas mehr als eine Exegese erlaubt und betrieben: „Was der große Meister uns sagen wollte?“ Ich neige aber sehr daran zu glauben, dass es einen „unglücklichen Umstand“ gibt, der wichtiger als alle anderen ist, warum es mit der Weiterentwicklung der Kreislauftheorie so langsam und mühsam vor sich ging. Was ich damit meine, sollen uns folgende drei Bilder zeigen.
Das erste Flussdiagramm entspricht den numerischen Beispielen der Tableau économique von Quesnay und das zweite den der Marxschen Reproduktionsschemata. Das Flussdiagramm rechts ist eine vereinfachte grafische Darstellung des numerischen Beispiels, das wir schon bei der Untersuchung des Transformationsproblems hatten. Die Flussdiagramme von Quesnay und Marx werden dem dreisektoralen Modell gegenübergestellt, um zu verdeutlichen, worin das schlechte Glück bei der Kreislauftheorie lag.
Der untere Sektor 2 bei Quesnay ist die Landwirtschaft, die mit Kapital arbeitet, mit dem sie sich durch die Schleife versorgt. Zu diesem Kapital gehört das Saatgut, so dass dieser Sektor (ungefähr) unserem ursprünglichen illustrativen Musterbeispiel mit dem Bauern und dem Boden entspricht. Dieser Sektor produziert auch Nahrung, was daraus zu schließen ist, dass ein Strom aus diesem Sektor die Wirtschaft verlässt. Dieser Sektor ist also zugleich auch Produzent von Konsumgütern. Ein Teil des Kapitals bezieht der Sektor 2 aber auch aus dem obigen Sektor 1, zu dem Manufakturen und Werkstätten gehören. Dazu gehören verschiedene, von den Bauern bei der Arbeit benutzte einfache Geräte und Werkzeuge - also Produktionsgüter. Der Sektor 1 ist also Kapitalproduzent, aber nicht nur. Er produziert auch Konsumgüter. Und nun schauen wir uns das berühmte Beispiel von Marx, in der Mitte der vorigen Darstellung, mit dem üblicherweise alle seine Analysen anfangen, an.
Es fällt sofort auf, dass Marx das Tableau économique nur vereinfacht hat. Er lässt den unteren Sektor seiner Reproduktionsschemata nur Konsumgüter zu produzieren, den obigen nur Produktionsgüter. Weil sich der Sektor 1 das Kapital (Produktionsgüter) selbst liefert, hat man bei ihm eine Schleife. In ihr sehe ich nun das Pech der alten Kreislauftheorie.
Warum hat Marx diese Schleife nicht weggelassen? Darüber kann man heute nur rätseln. Es ist durchaus denkbar, dass er sich gedacht hat, wenn man das Beispiel von Quesnay radikal vereinfacht, dann würde man auch einfacher und schneller zu irgendwelchen relevanten Schlussfolgerungen kommen. Und das war ein großer Irrtum. Marx hat dadurch alles sozusagen zusammengequetscht, so dass sich alles in seinen numerischen Beispielen „überlappt“, ein Gedanke geht in den anderen hinein, eine Größe verformt die andere, ... dies führt zur Verwechselung, und schließlich weiß man auf einmal nicht mehr, wo man steht ... und alles endet sehr schnell in einem Chaos.
Dass diese Schleifen bei Quesnay und Marx der Klotz am Bein der ganzen Kreislauftheorie waren, schließe ich aus eigener Erfahrung. Ich habe mehrere Jahre versucht, eine Systematik in den Beispielen von Marx zu finden, aber alle meine Versuche waren vergeblich. Ich erhoffte mir, einer aus der riesigen Zahl der Marxschen Interpreten - Marx als ein einzelner Autor hatte zeitlang mehr Anhänger als Mohammed - würde mir helfen. Es gibt zahlreiche Publikation, wo die Marxisten versucht haben, die Reproduktionsschemata zu erklären und zu vervollständigen, aber auch dort konnte ich keine Systematik erblicken. Das Vorgehen all dieser Interpreten war im Grunde dasselbe wie bei Marx: Sie fangen mit dem Gleichgewicht (der einfachen Reproduktion) an, dann fügen sie eine Annahme hinzu - die die weitere Richtung vorgegeben hat -, dann improvisieren sie, ab und zu fügen sie die nächste Annahme hinzu - die in die konkrete Situation gerade passt - dann wird weiter improvisiert ... Als ich daraus nichts gewinnen konnte, habe ich irgendwann - ich weiß jetzt selber nicht mehr wie und warum - ratlos und erschöpft aus dem Sektor 1 zwei Sektoren gemacht und die Schleife entfernt. So wie es das Bild rechts darstellt. Und dann war es plötzlich so, als ob jemand das Licht angemacht hätte.
Auf einmal wurde mir klar, dass die Beliebigkeiten bei Marx und seinen Interpreten damit zu tun haben, dass man die technischen Zusammenhänge der Produktion, die man untersuchte, völlig außer Acht ließ. Man wollte real-ökonomische Gesetzmäßigkeiten der Produktion erforschen, ohne dabei die produktionstechnischen Gesetzmäßigkeiten bzw. Notwendigkeiten zu berücksichtigen. Und das war falsch. Eine Möglichkeit die produktionstechnischen Gesetzmäßigkeiten zu berücksichtigen bzw. die ökonomische Analyse nicht gegen sie zu betreiben - was nur zu metaphysischen Halluzinationen führen kann - sind die distributiven Koeffizienten. Sie sind mir gleich in den Sinn gekommen, als ich mich der Schleife befreit habe. Und wenn die Idee oder das Prinzip schon da war, alles noch mathematisch zu artikulieren, war es nur noch eine Frage der Zeit und der Ausdauer. Zuerst habe ich alleine mit den distributiven Koeffizienten gearbeitet, dann hat sich herausgestellt, dass sie doch nicht immer ausreichen. Man kann nicht immer ohne technischen Koeffizienten auskommen. Aber der Ausbruch aus dem stationären Zustand war schon mit den distributiven Koeffizienten geschafft. Zusammen mit den technischen Koeffizienten steht nun eine strenge und starke analytische Methode zur Verfügung, mit der sich das ganze ökonomische System beliebig umgestalten lässt und damit sich seine verschiedenen Zustände untersuchen lassen.
Und die Schleife? Allgemein betrachtet lässt sich sie nicht ausschließen. Es kann bestimmt Sektoren geben, die wirklich für sich selbst Kapitalgüter produzieren. Wenn man sich aber mit dem Prinzip der distributiven Koeffizienten ein bisschen vertraut gemacht hat, sind diese Schleifen nicht das geringste Problem mehr. Und schon gar nicht sind sie es für einen versierten Mathematiker, der die Wirtschaft mit Gleichungen modelliert. Die Schleifen sind für ihn völlig normale distributive Koeffizienten, bei denen Indizien zwei gleiche Zahlen sind, mit denen man genauso wie mit allen anderen umgeht. Aber warum sollte man solche Schleifen, die dermaßen zur Verwirrung führen, in den Beispielen benutzen? Man muss es natürlich nicht, aber umsonst geht es nicht. Man muss dann einen zusätzlichen Sektor hinzunehmen. In unserem Fall hat man dann anstatt zwei drei Sektoren, wie im Beispiel oben rechts, aber das ist schon alles, was man tun muss.
Ein kreislauftheoretisches Musterbeispiel für eine Wirtschaft mit drei Sektoren
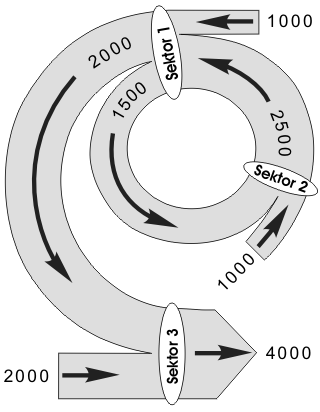
Das rechte Flussdiagramm gehört zum numerischen Beispiel, das wir schon benutzt haben - wie bereits erwähnt. Weil wir dieses Beispiel später immer wieder als Ausgangspunkt nehmen werden, ist es angebracht, es noch einmal vollständig darzustellen und ausführlich zu erörtern. Wir fangen mit einem vollständigeren Flussdiagramm an, mit dem sich manche der charakteristischsten Eigenschaften des Kreislaufmodells leichter verdeutlichen lassen.
| |
 |
|
| Distributive Koeffizienten: |
| δ |
|
1 |
2 |
3 |
| |
|
Sektor 1 |
Sektor 2 |
Sektor 3 |
| 1 |
Sektor 1: |
0 |
3/7 |
4/7 |
| 2 |
Sektor 2: |
1 |
0 |
0 |
| 3 |
Sektor 3: |
0 |
0 |
0 |
|
|
Aus dem Flussdiagramm lässt sich sofort entnehmen, dass sich alle Ströme irgendwann kreisförmig schließen. Dies ist also eine Möglichkeit, wie man sich ein Gleichgewicht vorstellen kann, wie gesagt, die älteste Möglichkeit in der ökonomischen Theorie. Man sieht deutlich bei jedem Sektor, dass seine Einnahmen (Angebot) und Ausgaben (Nachfrage) summarisch übereinstimmen. Das sind mikroökonomische Gleichgewichte. Wenn es bei jedem der Sektoren zu einer solchen Übereinstimmung kommt, kommt zugleich auch das makroökonomische Gleichgewicht zwischen dem gesamten Angebot und der gesamten Nachfrage auf dem Markt der Produktionsgüter zustande. Das makroökonomische Gleichgewicht auf dem Markt der Konsumgüter kommt dann zustande, wenn die Summe aller Nettoeinkünfte (die geöffneten Ströme bei jedem Sektor) gleich dem Wert aller Konsumgüter (bei uns die Produktion des Sektor 3) sind. Das ist bei uns auch der Fall.
Der Sektor 1 produziert Kapitalgüter, von denen der Sektor 2 einen Anteil von 3/7 und der Sektor 3 einen von 4/7 bekommt. Diese Anteile sind die distributiven Koeffizienten des Sektors 1: δ12 = 3/7 und δ13 = 4/7. Der Sektor 2 liefert seine ganze Produktion dem Sektor 1, so dass man hier nur einen distributiven Koeffizienten hat: δ21 = 1. Diese Koeffizienten bringen auf eine andere Weise das zum Ausdruck, was auch die technischen Koeffizienten besagen, dass die Güter in den Sektoren nach bestimmten Produktionsmethoden hergestellt werden.
Alle distributiven Koeffizienten unseres numerischen dreisektoralen Beispiels stehen in einer Tabelle rechts des obigen Flussdiagramms. (In der Mathematik würde man eine solche Tabelle als Matrix bezeichnen.) Wie merken, dass diese Tabelle ziemlich leer ist. Das kommt daher, dass die Wirtschaft unseres Beispiels sehr einfach strukturiert ist. Heben wir an dieser Stelle noch hervor, dass die Diagonale zwischen den Ecken links oben und rechts unten, wo die Koeffizienten mit gleichen Indizes stehen würden, völlig leer ist. Dass dort keine Zahl steht lässt uns wissen, dass keiner der Sektoren eine Schleife hat. Aber auch wenn wir eine Zahl bzw. eine Schleife hätten, wäre dies für die Mathematik ohne Belang. Schreibt man nämlich anhand dieser Koeffizienten ein Gleichungssystem, würde es keine Rolle spielen, ob die Indizes bei einigen Koeffizienten gleich sind oder nicht.
Es fällt sofort auf, dass bei jedem Sektor alle Nettoeinkünfte zu einer einzigen Größe zusammengefasst sind. Die Verteilung des Einkommens auf verschiedene Gruppen wird also außer Acht gelassen. Die Verteilung ist natürlich sehr wichtig - David Ricardo meinte sogar, sie zu untersuchen sei die wichtigste Aufgabe der ökonomischen Theorie -, sie ist aber nicht für das von Belang, was wir in den nächsten Beiträgen untersuchen werden. Deshalb wollen wir uns mit der Einkommensverteilung nicht unbedingt belasten. Ohne sie lässt sich der Produktionsprozess, der mit dem Flussdiagramm eindeutig bestimmt ist, einfacher und übersichtlicher darstellen, wie es die folgende Tabelle zeigt.
| |
| t |
Produktionsprozess |
| |
| Sektor 1: |
| Sektor 2: |
| Sektor 3: |
|
| |
K |
|
Ÿ |
|
Y |
|
| |
2500.00 |
+ |
1000 |
= |
3500.00 |
|
| |
1500.00 |
+ |
1000 |
= |
2500.00 |
|
| |
2000.00 |
+ |
2000 |
= |
4000.00 |
|
|
|
|
| Kapitalbeschaffung |
| für Reproduktionsperiode
t
+1 |
|
| |
K1t+1 |
= |
δ21 |
• |
Y2t |
= |
1 • 2500.00 |
= |
2500.00 |
|
| |
K2t+1 |
= |
δ12 |
• |
Y1t |
= |
3/7 • 3500.00 |
= |
1500.00 |
|
| |
K3t+1 |
= |
δ13 |
• |
Y1t |
= |
4/7 • 3500.00 |
= |
2000.00 |
|
|
|
|
Die Produktionsgüter, welche bei der Produktion verbraucht und verschlissen worden sind, müssen sich die Sektoren am Ende der Reproduktionsperiode wieder verschaffen, um am Anfang der nächsten Reproduktionsperiode ihre Produktion fortsetzen zu können. Diese Kapitalbeschaffung lässt sich mit Hilfe der distributiven Koeffizienten quantitativ bestimmen. Weil unsere Wirtschaft sehr einfach strukturiert ist und folglich nur sehr wenige distributive Koeffizienten hat, lässt sich auch die Kapitalbeschaffung sehr einfach ausrechnen, wie es rechts der obigen Tabelle dargestellt ist.
Unser Flussdiagram stellt einen stationären Zustand dar, also einen, der sich ohne Änderungen unendlich lange reproduzieren kann. Solche Zustände lassen sich kreislauftheoretisch auch mit technischen Koeffizienten (v 2.x) untersuchen. Diese Koeffizienten sind vor allem beim Vergleich verschiedener Gleichgewichtzustände von Bedeutung, womit sie die komparative Analyse oder komparative Statik beschäftigt. Distributive Koeffizienten machen die Untersuchung des Pfades möglich, der von einem Gleichgewichtszustand zum anderen führt. Sie sind somit die Grundalgen für eine dynamische Analyse der Funktionsweise der Marktwirtschaft. Das ist viel mehr als eine komparative Statik. Deshalb spreche ich vom Kreislaufmodell Version 3.0.
Bei der Untersuchung des dynamischen Gleichgewichts - wo man unter anderem mit Sparen, Akkumulation und Nachfragemangel zu tun hat -, werden noch andere Größen und damit noch zusätzliche Zahlen berücksichtig werden müssen. Um dann die Übersicht nicht zu verlieren, werden wir uns noch mit Tabellen einer anderen Art weiter helfen. Diese Tabelle würde uns für das gerade dargestellte Beispiel, weil es einfach ist, kaum etwas bringen. Aber zur Vervollständigung zeigen wir sie trotzdem.
Aus der Tabelle ist für jeden Sektor nachvollziehbar, dass er genau so viel liefert bzw. anbietet (linke Hälfte) wie er empfängt bzw. nachfragt (rechte Hälfte). Später, wenn noch andere Größen dazu kommen, werden sich andere wichtige Zusammenhänge verdeutlichen lassen.
|
|
|